City of toronto maintains a variety of interesting datasets on open.toronto.ca/datasets . In this article I explore the Active Permits and Cleared Permits datasets which contain records of all building permit applications of Toronto since 2000.
let’s start by loading the active permits dataset and taking a look at the features. I recommend you take a look at the readme file as well.
permits = pd.read_csv("datasets/activepermits.csv")
Index(['PERMIT_NUM', 'REVISION_NUM', 'PERMIT_TYPE', 'STRUCTURE_TYPE', 'WORK',
'STREET_NUM', 'STREET_NAME', 'STREET_TYPE', 'STREET_DIRECTION',
'POSTAL', 'GEO_ID', 'WARD_GRID', 'APPLICATION_DATE', 'ISSUED_DATE',
'COMPLETED_DATE', 'STATUS', 'DESCRIPTION', 'CURRENT_USE',
'PROPOSED_USE', 'DWELLING_UNITS_CREATED', 'DWELLING_UNITS_LOST',
'EST_CONST_COST', 'ASSEMBLY', 'INSTITUTIONAL', 'RESIDENTIAL',
'BUSINESS_AND_PERSONAL_SERVICES', 'MERCANTILE', 'INDUSTRIAL',
'INTERIOR_ALTERATIONS', 'DEMOLITION'],
dtype='object')
Most frequent types of permits
permits["PERMIT_TYPE"].value_counts().iloc[:10].plot(kind="bar",rot=90)
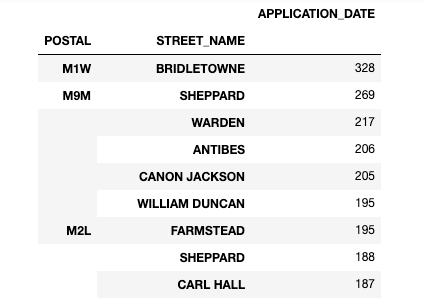
Most frequent street names
permits["STREET_NAME"].value_counts().head(10)
YONGE 5433
SHEPPARD 3819
BLOOR 3310
DUNDAS 3092
KING 3074
QUEEN 2965
LAWRENCE 2352
BAY 2160
EGLINTON 2140
ST CLAIR 1884
Name: STREET_NAME, dtype: int64
Contributions of occupancy
the last columns in the table are the square meters of the area for each type of occupancy. for example one of the permits has 157.00 square meters of RESIDENTIAL occupancy.
here are the percentages for the whole table.
occupancy = permits.loc[:,"ASSEMBLY":].sum(axis=0)
occupancy = round((occupancy/ occupancy.sum()) *100,2)
occupancy.sort_values(ascending=False).astype(str) + "%"
RESIDENTIAL 42.95%
INTERIOR_ALTERATIONS 18.01%
INDUSTRIAL 15.39%
BUSINESS_AND_PERSONAL_SERVICES 12.17%
DEMOLITION 5.48%
ASSEMBLY 2.58%
MERCANTILE 1.94%
INSTITUTIONAL 1.47%
dtype: object
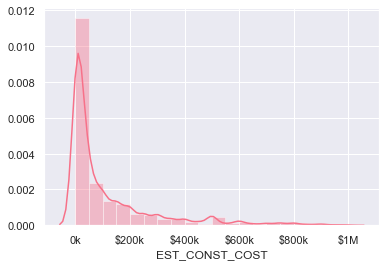
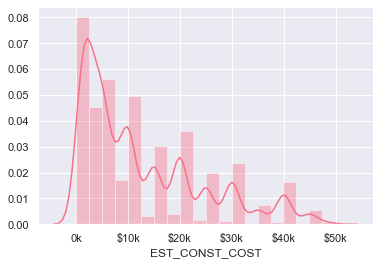
Distribution of construction cost
Here we scale the construction costs to $1/1000 and then limit it to under 2 million dollars. The mean turns out to be at $506k and there are some picks on rounded values like $10k, $20k, $30k.
cost = permits["EST_CONST_COST"].dropna()
cost = cost[ cost.str.isnumeric()].astype(float)
cost /= 1000 # scale it to thousands of dollars
cost = cost[(cost>0) & (cost<1000)]
# cost = cost[(cost>0.001) & (cost<50)] # under $50k
ax = sns.distplot(cost,bins=20)
# ax.set(xticklabels=["","0k","$10k","$20k","$30k","$40k","$50k"])
ax.set(xticklabels=["","0k","$200k","$400k","$600k","$800k","$1M"])
cost.describe()
count 89657.000000
mean 506.999859
std 6607.660147
min 0.000000
25% 1.000000
50% 15.000000
75% 120.000000
max 595875.683000
Name: EST_CONST_COST, dtype: float64
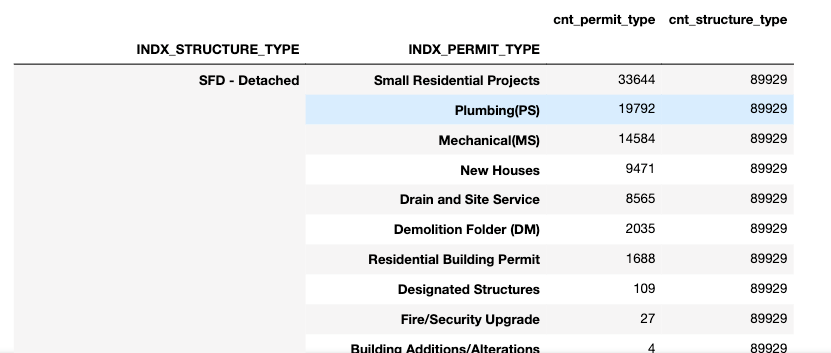
Most frequent structure types and permit types
pd.set_option('display.max_rows', 1000)
structure_permit_groups = permits.groupby(["STRUCTURE_TYPE","PERMIT_TYPE"])\
.agg({ "PERMIT_TYPE":"count"})
structure_permit_groups.index.names=["INDX_STRUCTURE_TYPE","INDX_PERMIT_TYPE"]
structure_permit_groups["cnt_structure_type"] = structure_permit_groups.groupby(["INDX_STRUCTURE_TYPE"])\
.transform(np.sum)
structure_permit_groups.columns = ["cnt_permit_type","cnt_structure_type"]
structure_permit_groups = structure_permit_groups.sort_values(["cnt_structure_type","cnt_permit_type"]
,ascending=False)
Trend of permits over time
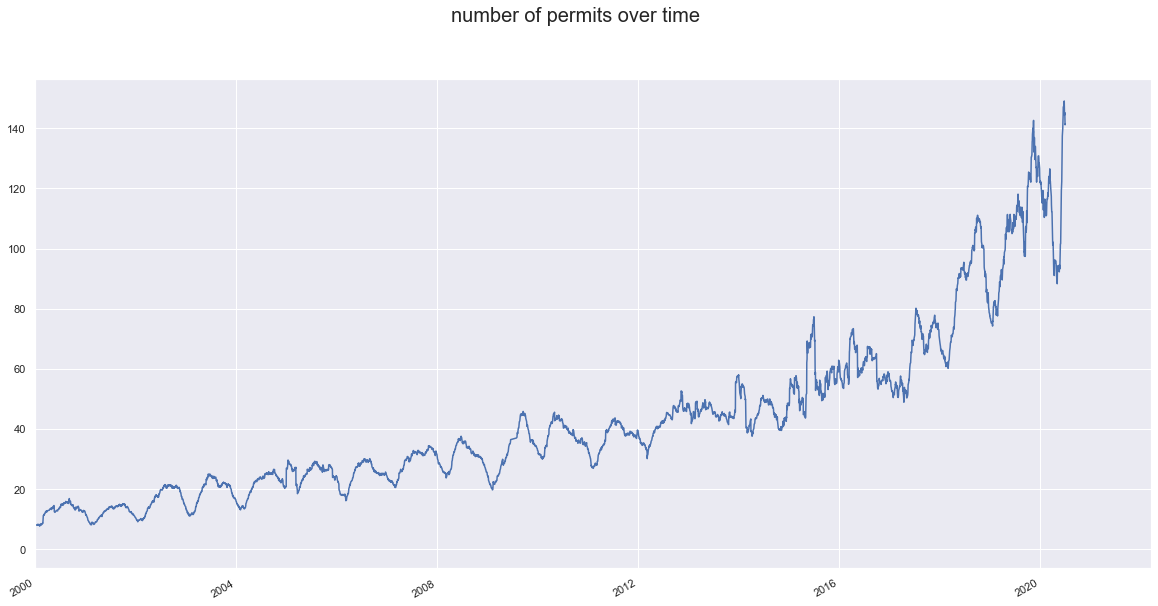
our main goal for this article is to gain some perspective on how the number and proportions of permits are changing over time. we start by looking into aggregate number of all permits together. The seasonal pattern is pretty interesting but doensn’t tell us anything about whats happening in each category .
permits["APPLICATION_DATE"] = pd.to_datetime(permits["APPLICATION_DATE"],format="%Y%m%d000000")
dates = permits["APPLICATION_DATE"].value_counts()
dates = dates.sort_index()
fig, ax = plt.subplots(1)
fig.suptitle("number of permits over time",fontsize=20)
dates.rolling(50).mean().plot(figsize=(20,10),ax=ax)
ax.set_xlim(pd.Timestamp("2000-01-01"))
Categories of permits and their trend over time
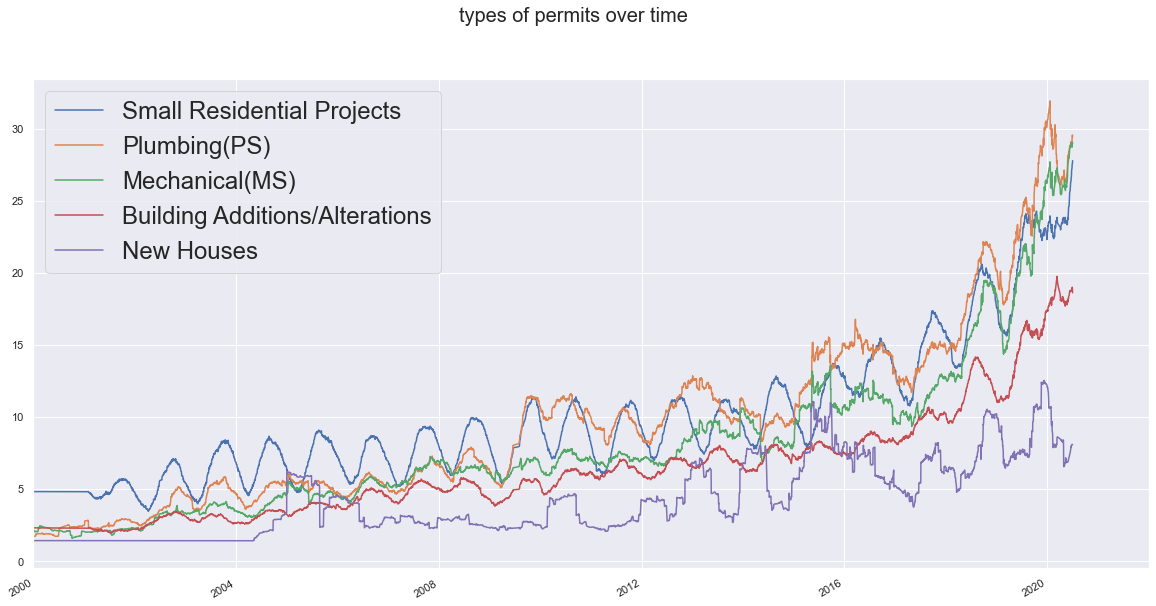
First we find the most active types of permits. and then we can go ahead and plot each of them and see how they’re changing together.
frequent_permit_types= permits["PERMIT_TYPE"].value_counts().iloc[:5].index.tolist()
frequent_permit_types
['Small Residential Projects',
'Plumbing(PS)',
'Mechanical(MS)',
'Building Additions/Alterations',
'New Houses']
fig, axes = plt.subplots(1,figsize=(20,10))
fig.suptitle("types of permits over time",fontsize=20)
sns.set_palette("husl")
for i,permit_type in enumerate(frequent_permit_types):
type_trend = permits[permits["PERMIT_TYPE"]==permit_type]["APPLICATION_DATE"].value_counts()
type_trend.sort_index(inplace=True)
ax = type_trend.rolling(100).mean().plot(label=permit_type)
ax.set_xlim(pd.Timestamp("2000-01-01"))
plt.legend( prop={'size': 24})
The seasonal trend of Small Residential Projects is pretty strong. which totally makes sense in the case of outdoor projects. let’s take a look at the work column:
permits[permits["PERMIT_TYPE"]=="Small Residential Projects"]["WORK"].value_counts()
Multiple Projects 18437
Interior Alterations 7563
Addition(s) 6978
Garage 3504
Party Wall Admin Permits 3299
Other(SR) 2702
Porch 2099
Deck 1916
Underpinning 1731
Unknown 1413
Accessory Building(s) 820
Second Suite (New) 715
Walk-Out Stair 651
Fire Damage 532
Finishing Basements 389
Carport 326
Canopy 281
New Laneway / Rear Yard Suite 111
Pool Fence Enclosure 98
Types of CURRENT_USE
the CURRENT_USE column gives us a good insight on what most of these permits are all about. let’s take a quick look at the most frequent ones.
permits["CURRENT_USE"].value_counts().head(20)
Sfd 48593
Vacant 26441
Office 14141
Sfd-Detached 10851
Single Family Dwelling 6513
Retail 5993
Sfd - Detached 4917
Apartment Building 3835
Sfd Detached 3620
Sfd-Semi 2767
Industrial 2596
Apartment 2186
Vacant Land 1997
Restaurant 1997
Hospital 1657
Sfd-Townhouse 1284
House 1276
Single Family Detached 1236
Retail Store 1235
Sfd Semi 1235
Name: CURRENT_USE, dtype: int64
Focusing on new houses and new buildings
let’s take a look at the zip codes and streets with the most permit applications. later on we’ll talk about how this can be important.
new_buildings = permits[permits["PERMIT_TYPE"].isin(["New Building","New Houses"])]
active_zips = new_buildings.groupby(["POSTAL","STREET_NAME"]).agg({"APPLICATION_DATE":"count"})\
.sort_values("APPLICATION_DATE",ascending=False)
display(active_zips.iloc[1:100])
zips = permits["POSTAL"].unique()
array(['M2R', 'M4L', 'M6R', 'M6K', 'M6H', 'M5C', 'M4K', 'M6P', 'M2N',
'M2P', 'M1S', 'M6B', 'M9C', 'M5B', 'M2J', ' ', 'M5J', 'M8V',
'M5P', 'M3A', 'M5G', 'M5T', 'M4G', 'M3M', 'M9W', 'M8Z', 'M5M',
'M4M', 'M4E', 'M6J', 'M6G', 'M4Y', 'M5V', 'M2L', 'M8Y', 'M4W',
'M4N', 'M6L', 'M9A', 'M4V', 'M5N', 'M2M', 'M1L', 'M4T', 'M6S',
'M6C', 'M5A', 'M4C', 'M9B', 'M3C', 'M5S', 'M4B', 'M9V', 'M1P',
'M6A', 'M4A', 'M6E', 'M6N', 'M8X', 'M4P', 'M3B', 'M3H', 'M4R',
'M6M', 'M5H', 'M3J', 'M9M', 'M8W', 'M1C', 'M2H', 'M9R', 'M9N',
'M4J', 'M1E', 'M5R', 'M4X', 'M3N', 'M4S', 'M5E', 'M5X', 'M2K',
'M9L', 'M1X', 'M1B', 'M3L', 'M3K', 'M9P', 'M1N', 'M1T', 'M1G',
'M1K', 'M7A', 'M1J', 'M1H', 'M1R', 'M1M', 'M1W', 'M4H', 'M1V'],
dtype=object)
Most active zip codes over time
here we start by finding and sorting the most active zip codes, based on the total number of applications. and then we get the top 10 and look into their trend over time. filtering out the most active zip codes gives us meaningful trends.
most_active_zips = new_buildings.groupby(["POSTAL"])\
.agg({"APPLICATION_DATE":"count"})\
.sort_values("APPLICATION_DATE",ascending=False)
most_active_zips = most_activezips.index[1:10]
Daily_Count_zipcodes = new_buildings.groupby([pd.Grouper(key="APPLICATION_DATE",freq="M"),"POSTAL"])\
.agg({"POSTAL":"count"})
Daily_Count_zipcodes.columns = ["POSTAL_COUNT"]
Daily_Count_zipcodes.reset_index(1,inplace=True)
# Daily_Count_zipcodes
fig, ax = plt.subplots(1,figsize=(20,15))
for zip_code in most_active_zips:
Daily_Count_zipcodes[Daily_Count_zipcodes["POSTAL"]==zip_code]["POSTAL_COUNT"]\
.rolling(20).mean().plot(ax=ax,label=zip_code)
ax.set_xlim(left=pd.Timestamp("2007-01-01"))
plt.legend( prop={'size': 24})
plt.xticks(fontsize=24)